戒烟一个月了,感觉还不错,找时间讲讲心路历程。
这次戒烟比较有信心,因为是一次认知升级。
这次更像是,我可以不抽烟了,这件事对我来说理所当然,没有压力。我不会觉得不吸烟是一个挑战,是一件需要耗尽全部的意志力和用尽各种办法才能达到的事情。
很有趣的经历。
戒烟一个月了,感觉还不错,找时间讲讲心路历程。
这次戒烟比较有信心,因为是一次认知升级。
这次更像是,我可以不抽烟了,这件事对我来说理所当然,没有压力。我不会觉得不吸烟是一个挑战,是一件需要耗尽全部的意志力和用尽各种办法才能达到的事情。
很有趣的经历。
答辩结束了,昨晚和师弟师妹们吃了顿好的。昨天情绪一直很不稳定,现在还比较平静。
答辩现场老师们还比较温和,但是自我感觉极差,一是讲得比较不流畅,二是没什么内容。自己两个工作,第一个工作压根没人问问题,第二个工作,问了跟辐射机制有关的问题,我答得不太好。
暴露的问题就是,基础太差,对文章积累太少,物理图像几乎没有。然而我还是过了,按照肖师兄的话来说,我这博士期间给自己没有一个交代。
知耻后勇还是及时止损?
昨天刚过了27的生日,没什么仪式感,在床上趴了一天。
生日前一天,刘洋硬把我拉去打羽毛球,我自己一时大意把腰伤着了。对刘洋怨念了两天,今天没那么生气了。今天主要想的是以后怎么把体重减下来。
27岁了,是不是要开始盘算规划些什么了,我不知道,希望答辩完以后,能重新开始新篇章吧。
今天是每周的组会日,上午是学生的进展汇报,下午是慧眼的文章进展会。说实话,这周没有什么进展,上午糊弄过去了,说我在写毕业论文;下午也糊弄过去了,FRB180916 的慧眼观测,给出了慧眼的流量上线,这个工作主要是依赖慧眼本底组的结果,因为这个源其他的X射线探测器没有看到信号,慧眼基本上也看不到信号,所以关键是要把本底调合理。
中午跟廖进元进行了沟通,希望他介绍本底更新的情况,让他讲讲,顺便把我的FRB处理的结果介绍一下,其实本意是因为实在不想在这个组会发言。但廖拒绝了,无语。于是在组会上,我用了一句话介绍了我的工作,说更新了结果本底,最后能给出上限。然后坑了廖一手,在视频会议中,问廖是否有补充。廖也一时语塞,显然是没有意料到。
周期性地陷入迷惘之中,没有工作的动力,缺乏读书的精神,总之很颓靡。近期和廖师走的比较近,部分原因是因为在时政观点上的某种契合。
而这种契合,不是在具体事物评价上的观点一致,而是有一个共识——政府是该被批评的。虽然在批评的激烈程度上,我和廖师都有极大的差异,我比较温和,追求的是宪政和改良。而廖师的观点是,共产党就是土匪。这种表述,我认为是带有情绪的,当然他有他的历史依据和事实依据,但往往在交流的过程中这种态度的差异让我感到十分尴尬。
今天发现 EPUB 格式的文件具有十分优秀的标注功能,结合Kindle和iPad,可以比较方便地同步和导出,很爽。
最近诸事不顺,毕业准备延期到8-9月份答辩,论文才刚开始,工作也没有着落。
特别是疫情以来,巨大的认知偏差,讨论过程中共识的缺乏,让我感到很沮丧。
我打算开始恢复祷告,不是期待这样做有用,而是深深感到自己的智慧远不足以应付纷杂的思路,时常感到无法沉静下来思考问题。
今天路上碰到我老板,正准备自己去医院。一瘸一拐的,面部表情有些痛苦。我也闲着,就陪他去医院了。原来他也是腰椎间盘突出,压迫神经还比较严重那种。
他拍完CT,我俩坐着等胶片,半个多小时,沉默。偶尔灵光一现想出一个能聊的问题,双方也很快把话聊死。我还比较镇定,在脑子里回放了一遍“银翼杀手2049”,还私自给K和Joey加了几场床戏。
看完病,取完药,我俩走出医院。
“您这情况,我觉得还是手术比较好。”
“还是保守治疗吧。”
“我没这么严重恢复了大半年,我估计您这一时半会儿缓不过来,得歇着。”
他沉默了一秒,说了一句“嗯”。
北京的冬天可真冷,我也不那么讨厌他了。
设
为连续随机变量,上下限是
和
,若存在连续非负实函数
,对任何实数
成立:
为概率密度函数或概率密度。
用离散的情况去理解概率密度函数会更直观。为各随机变量的概率(连续的情形下则为概率密度)
为
个随机变量之和(独立随机变量的概率满足加法律)。
在和龙曦讨论一个“置信水平”和“置信区间”的问题过程中,对于参数估计中的置信区间的报道有了新的理解,而之前的理解在遇到一些问题时会出现错误。这里首先讲讲参数估计中置信区间的问题,然后介绍Bootstrap的方法,并用Bootstrap抽样作为例子解释置信区间的问题。
待估参量 (真值也记为
)的一个样本
作为参数
的估计值
。
若估计值 落入真值左右某个区间
的概率为
:
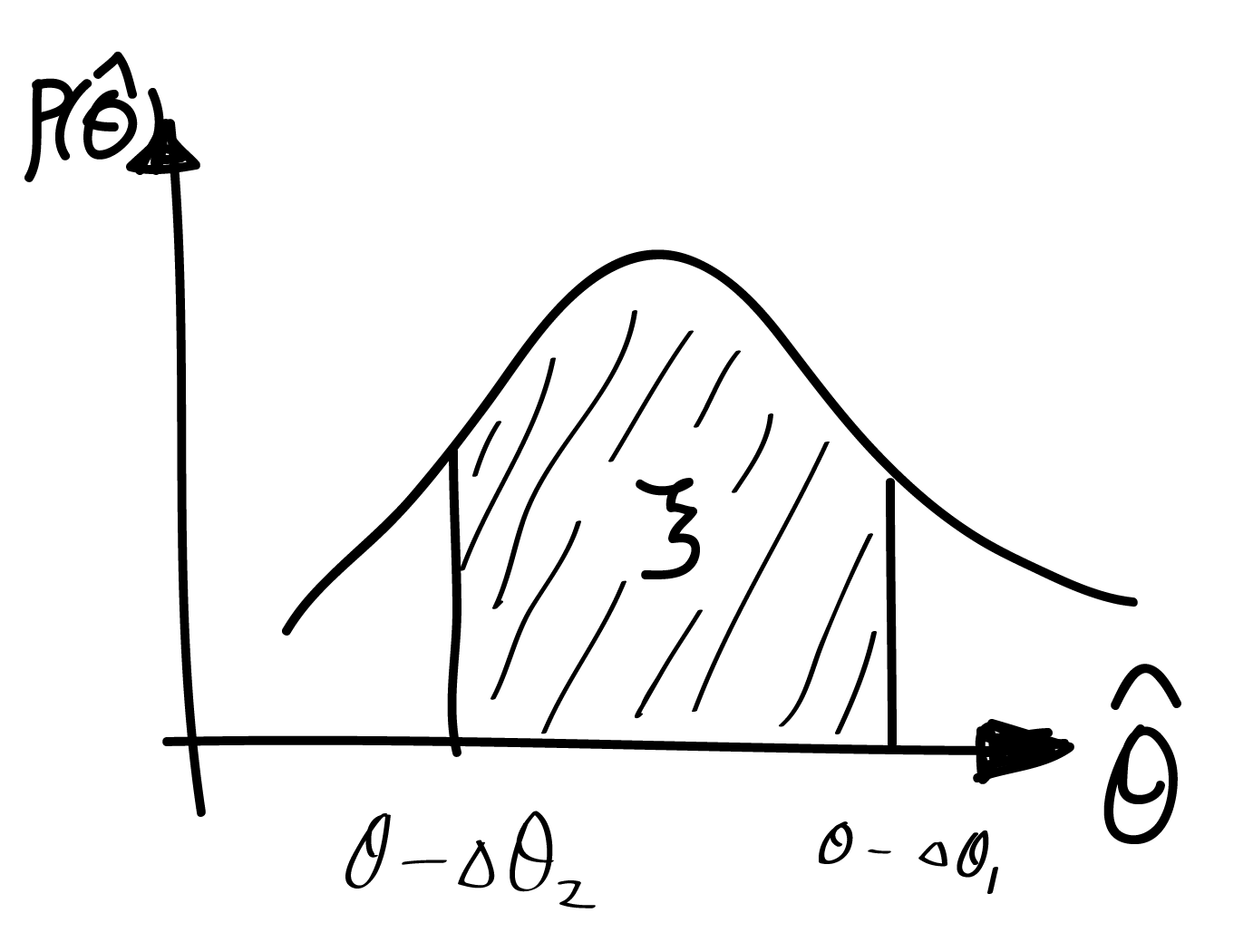
将不等式移项可得
即:在估计值 左右的一个区间
内,包含参数真值
的概率也是
。参数估计的结果报道为:
Note: 在报道结果的时候,报道的是待估参量 ,而样本的估计值的概率区间与真值的概率区间是不一致的,注意这里的区别。如果区间不是对称的,则报道值会出现错误。
若待估参量的样本有限,不能很好的反映待估参量的统计结果,则可使用Bootstrap方法进行抽样。用一组样本,进行重采样,得到基于这个样本的多个样本,对样本进行统计,得到待估参量的估计值。
举个例子。已知样本是 ,我们考虑样本的平均值的估计量。该样本的平均值是6。我们对这个样本进行bootstrap重采样,即以
为样本空间,产生多组样本(这里产生5组)。我们对于重采样的样本
将 参考样本
视为待估参量
。重采样样本的均值与参考样本的平均值的差值的分布为 -3, -2, 0, 1, 1。
若在 60% 的置信水平上,估计值 的置信区间是 (-2, 0, 1),
则待估参量
的置信区间是
。这里的待估参量则是真值,不是第一组参考样本的估计量,而这里的估计值则是第一组参考样本的估计量,所以
(置信水平 60%)