GRM Python tools development Plan

Posted on 2021-11-11 by Youli

The Alpha Version of grmtools implements a framework that can satisfy basic data processing. The data processing mainly consists of the following, the main goal is to finish developing the reasonable algorithm for GRB analysis. And the pipeline for GRM data products should also be built.

Spectrum fitting (integrating the use of pyXspec) and generating the products related to spectra. (DUE 2021.11.30)
- spectrum fitting by specific model
- calculate Energy Flux and Photon Flux

Create the light curve and the products related to light curves.
- Count Light
- Cumulative Light curve
- Background selection and background fitting (DUE 2021.12.30)
- Hardness ratio
- Time delay of two light curve (DUE 2022.01.30)
- Implement an algorithm to find the peak of the light curve and calculate the peak Energy/Photon flux of the peak (DUE 2022.02.30)

pipeline module that implemented for the GRM products (defined GRM SP products in grm-product-generator) (DUE 2022.04.30)
- pipeline algorithm of selecting background and fitting background
- pipeline algorithm of fitting the time-resolved and time-integrated spectra and save the scientific results to proper FITS files.
- Create all products required for GRM SP products

Bootstrap方法以及更正一些错误的理解

Posted on 2017-12-03 by Youli

在和龙曦讨论一个“置信水平”和“置信区间”的问题过程中，对于参数估计中的置信区间的报道有了新的理解，而之前的理解在遇到一些问题时会出现错误。这里首先讲讲参数估计中置信区间的问题，然后介绍Bootstrap的方法，并用Bootstrap抽样作为例子解释置信区间的问题。

一、区间估计（李惕培《实验的数据处理》）

待估参量 $\theta$ （真值也记为 $\theta$ ）的一个样本 $(x'_1, x'_2, \cdots , x'_N)$ 作为参数 $\theta$ 的估计值 $\hat{\theta}(x'_1, x'_2, \cdots , x'_N)$ 。

若估计值 $\hat{\theta}$ 落入真值左右某个区间 $[\theta-\Delta\theta_2, \theta + \Delta\theta_1]$ 的概率为 $\xi$ ：

$\xi = P_r(\theta - \Delta\theta_2 \leqslant \hat{\theta} \leqslant \theta + \theta_1)$

Screen Shot 2017-12-03 at 7.57.36 PM

将不等式移项可得

$P_r(\hat{\theta} - \Delta\theta_1 \leqslant \theta \leqslant \hat{\theta} + \Delta\theta_2) = \xi$

即：在估计值 $\hat{\theta}$ 左右的一个区间 $[\hat{\theta} - \Delta\theta_1, \hat{\theta} + \Delta\theta_2 ]$ 内，包含参数真值 $\theta$ 的概率也是 $\xi$ 。参数估计的结果报道为：

$\theta = \hat{\theta}^{+\Delta\theta_2}_{-\Delta\theta_1}$

Note: 在报道结果的时候，报道的是待估参量 $\theta$ ，而样本的估计值的概率区间与真值的概率区间是不一致的，注意这里的区别。如果区间不是对称的，则报道值会出现错误。

二、Bootstrap 方法

若待估参量的样本有限，不能很好的反映待估参量的统计结果，则可使用Bootstrap方法进行抽样。用一组样本，进行重采样，得到基于这个样本的多个样本，对样本进行统计，得到待估参量的估计值。

举个例子。已知样本是 $\hat{\theta} ( 1,3,5,7,9,11)$ ，我们考虑样本的平均值的估计量。该样本的平均值是6。我们对这个样本进行bootstrap重采样，即以 $\hat{\theta''}( 1,3,5,7,9,11)$ 为样本空间，产生多组样本（这里产生5组）。我们对于重采样的样本 $\hat{\theta''}$ 将参考样本 $\hat{\theta}$ 视为待估参量 $\theta$ 。重采样样本的均值与参考样本的平均值的差值的分布为 -3, -2, 0, 1, 1。

若在 60% 的置信水平上，估计值 $\hat{\theta}$ 的置信区间是 (-2, 0, 1)， $\Delta\theta_2 = 2, \Delta\theta_1 =1$ 则待估参量 $\theta$ 的置信区间是 $[\hat{\theta}-\Delta\theta_1, \hat{\theta}+\Delta\theta_2]$ 。这里的待估参量则是真值，不是第一组参考样本的估计量，而这里的估计值则是第一组参考样本的估计量，所以

$\theta = \hat{\theta}^{+\Delta\theta_2}_{-\Delta\theta_1}=6_{-1}^{+2}$ （置信水平 60%）

Deducing GJ electron density

Posted on 2017-03-10 by Youli

Prove that plasma density surrounding Neutron Star follows:
$\rho = \frac{\nabla\cdot \vec{E}}{4 \pi c}= \frac{-\vec{\Omega} \cdot \vec{B}}{2 \pi c }\frac{1}{1-(\Omega r/c)^2 \sin^2 \theta}$
because the Lorentz force vanish here, we have:
$\vec{E} = - \frac{\vec{\Omega}\times \vec{r} \times \vec{B}}{c}$
So,
$\frac{1}{4\pi} \nabla \cdot \vec{E} = - \frac{1}{4\pi} \nabla \cdot (\frac{\vec{\Omega}\times \vec{r} \times \vec{B}}{c}) = - \frac{1}{4\pi} \nabla \cdot [\frac{(\vec{\Omega}\times \vec{r}) \times \vec{B}}{c}]$
make use of vector formulas, we obtain
$\frac{1}{4\pi} \nabla \cdot \vec{E} = - \frac{1}{4\pi} \left\{ \vec{B} \cdot [ \nabla \times \frac{ \vec{\Omega} \times \vec{r}} {c}] - \frac{(\vec{\Omega}\times \vec{r})}{c} \cdot (\nabla \times \vec{B}) \right\}$
due to the Maxwell’s equation $\nabla \times \vec{B} = 4 \pi \vec{J} = 4 \pi q \vec{\beta_t} = \frac{\vec{\Omega} \times \vec{r}}{c} \cdot (\nabla \cdot \vec{E})$
Thus,
$\frac{1}{4\pi} \nabla \cdot \vec{E} = - \frac{1}{4\pi} \left\{ \vec{B} \cdot [ \nabla \times \frac{ \vec{\Omega} \times \vec{r}} {c}] - (\frac{\Omega r \sin \theta}{c}\vec{\phi}) (\frac{\Omega r \sin \theta}{c}(\nabla \cdot \vec{E})\vec{\phi}) \right\}$

so,
$[1-(\Omega r/c)^2 \sin^2 \theta] \frac{\nabla \cdot \vec{E} }{4 \pi} = - \frac{1}{4\pi} [\vec{B}\cdot(\nabla \times \frac{\Omega r \sin \theta}{c} \vec{\phi})]$
where, $\nabla \times \frac{\Omega r \sin \theta}{c} \vec{\phi}$ can be calculated by $\nabla$ calculator as spherical coordinate form:

$\nabla \times \frac{\Omega r \sin \theta}{c} \vec{\phi} = \frac{1}{r \sin \theta}[\frac{ \partial}{\partial \theta}(\sin \theta \frac{\Omega r \sin \theta}{c})- \frac{\partial 0 }{\partial \phi}] \vec{e_r} + \frac{1}{r}[\sin \theta \frac{\partial 0 }{\partial \phi} - \frac{\partial}{\partial r} ( r \frac{\Omega r \sin \theta}{c})]\vec{e_{\theta}} + \frac{1}{r}[\frac{\partial}{\partial r}(r 0) - \frac{\partial 0 }{\partial \theta}] \vec{e_{\phi}}$
$\nabla \times \frac{\Omega r \sin \theta}{c} \vec{\phi} = \frac{2\Omega \cos \theta}{c} \vec{e_r} - \frac{2 \Omega r \sin \theta}{c} \vec{e_{\theta}}$
$\nabla \times \frac{\Omega r \sin \theta}{c} \vec{\phi} = \frac{2}{c} \vec{\Omega}$
Therefore,
$[1-(\Omega r/c)^2 \sin^2 \theta] \rho = - \frac{1}{4 \pi}(\vec{B} \cdot \frac{2}{c}\vec{\Omega})$

finally, we obtain
$\rho = \frac{-\vec{\Omega} \cdot \vec{B}}{2 \pi c }\frac{1}{1-(\Omega r/c)^2 \sin^2 \theta}$

Fermi analysis tool for MacOS Sierra

Posted on 2017-03-01 by Youli

JUST download source distribution of Fermi analysis tool for OS X el capitan, and compile it.

It works perfectly on MacOS Sierra as well.

Fermi data analysis notes on Pulsar

Posted on 2016-10-19 by Youli

The flux of quiescent state of Crab Nebular in a time interval of 360 days over a ten-year observation was obtained utilizing Fermi data. The fluxes of point sources in ROI (region of interest) are written in file *results.fits generated by Fermi tool gtlike .

The detail of analysis thread can be found here. However, there were problems not reported in the instruction.

1. Environmental variables

The source model XML file was generated by user donated Python script make3FGLxml.py. Before this process, the event data was selected, the counts map was generated, and the newest version of diffuse models was downloaded from Fermi website.

Because of some unknown glitches, the following steps are required to run make3FGLxml.py successfully:

after compiling Fermi environment by doing

$ fermiinit

$ which python

the path of Python compiler (I’m not sure how to call it) is set to ~/Documents/Fermi/ScienceTools-v10r0p5-fssc-20150518-x86_64-unknown-linux-gnu-libc2.19-10/x86_64-unknown-linux-gnu-libc2.19-10/bin/python

set a link for this path to the path of /usr/bin/python by doing:

$ ln ./python /usr/bin/python

By doing those processes, python script for generating source model XML file is ready to go.

2. Script input parameters

When running gtlike, a bizarre problem occurred: buffer overflow detected, and the process was terminated. We spent a lot of time debugging, and it turns out that the solution is to simplify the input parameters of running python script. I suggest running make3FGLxml.py in the path of point source file gll_psc_v16.fit. In this case, cut the absolute path of point source file to simplify the input parameters.

$ python make3FGLxml.py gll_psc_v16.fit …

3. Another Environmental variables problem

The last step of spectral fitting processes is to use HEASOFT tool farith to subtract model source counts map from observed counts map. The HEASOFT environment is required

$ heainit

Setting heainit environment when finishing all Fermi analysis processes, which includes gtselect, gtmktime, gtbin, gtltcube, gtexpcube2, gtlike, gtmodel, is recommended.

log20150905

Posted on 2016-09-06 by Youli

do gtselect

gtselect

@events.txt

crab_region_filtered.fits

83.633221

22.014461

3

239557500

274117500

100

300000

105

RA and DEC are generated from gtephem with start time of 239557500;

radius of new search region is 3 degree;

observation period is 400 days started by 239557500 (MET);

energy range: 100 MeV – 300 GeV; maximun zenith angle value is 105 degree.

do gtmktime

gtmktime

spacecraft.fits

(IN_SAA!=T && DATA_QUAL==1 && LAT_CONFIG==1 && ABS(ROCK_ANGLE)<52

yes

crab_region_filtered.fits

crab_gtmktime.fits

after gtmktime, do barycentering time correction

gtbary

crab_gtmktime.fits

spacecraft.fits

crab_event_bary.fits

83.633221

22.014461

while time range of spacecraft.fits which is 239557417-494731078 covers selected time period.

frequency search by python

no good chi_square.

observation period set to 30days and 400days, no good.
radius of search region in gtselect process set to 0.5 degree, no good.

log20160818

Posted on 2016-08-21 by Youli

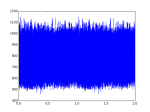
明早作报告，天呐，今晚又要加班了。记录下这两天学到的东西和工作

1. RXTE 数据处理流程

数据下载，在 HEASARC 网站 Archive 目录下选中 Browse Mission Interface

我也不知道，这么无脑的东西，我截屏说明一下是为什么。我们直接到 RXTE 的 PCA 数据处理流程好了。

1.1 PCA 数据预处理

总体的思路是为了筛选出我们需要的数据文件，然后可通过 fasebin 以及 fbssum 折叠轮廓，或者使用得到的数据文件自己对数据处理得到脉冲轮廓。

$ heainit

$ xdf

点击 Reset -> 选中 FTP NO File -> 地址选择当前文件夹（.）或者填写绝对路径 -> 点击 Save -> 点击 Make ObsList

注意：点击 Make Obslist 显示申请观测号之前，不能选中 Time Range 或是 Subsystems 中的选项，否则会导致无法生成观测号。

点击 Make ObsList -> 在 Observation 中选中观测号 -> 选中 PCA -> 点击 Make AppIdConfigList -> 选择数据模式 -> 点击 Make FileList -> 输入保存的文件名 -> 点击 Save Filelist

指定目录下生成了提取出的对应观测号以及仪器下的数据文件（.xdf）。

$ maketime filename.xfl gti

通过给定的判据+过滤文件，筛选出数据的“好时间段”。其中过滤文件（.xfl）在 stdprod 中直接拷贝，判据（expression）：elv.gt.10.and.offset.lt.0.02

在对单独的观测号处理时，判据没给出 pcu 的开关，默认 pcu 五个全开。在批处理（Rex）中会得到更加准确的 expression，包含了 pcu 信息。

$ fselect (.xdf中指定的文件) gtifilter_file “gtifilter(‘git’)”

通过好时间文件筛选出好时间数据。

$ fselect gtifilter_file fselect_file @bitfile

利用 bitfile 进一步筛选需要的时间文件

bitfile 的内容和格式：

以 crab 脉冲星 RXTE 96802-01-18-00 观测号为例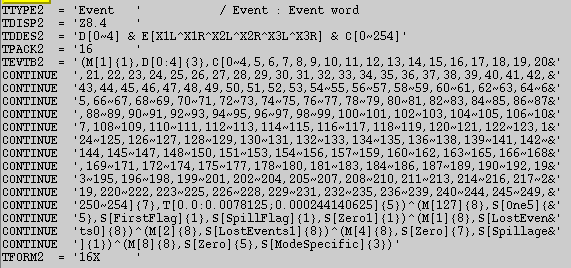： Screen Shot 2016-08-19 at 2.06.19 AM.png

Event == b1_ _ _ xxxxxxxxx 通过二进制编码表征一些标记，包括 M 标记事例是真事例还是时钟信号，{1} 表示占 1 位编码。D 标记 PCU 的开关情况，[0:4] 表征？{3} 占3位二进制码。C 是筛选能道，可以使用逻辑运算符选择能道区间。 E 标记探测器的阳极丝。

太阳系质心修正

$ faxbary fselect_file faxbary_file ./orbit/orbitfile ra=sourceRA dec=sourceDEC

由于关注的是源的周期性相关的物理信息，所以需要将光子到达探测器的时间，转换到到达太阳心质心的时间。否则光子信号会有一个与卫星的轨道以及地球的轨道有关的一个周期叠加。

生成质心修正后的示例型文件，至此，可以自行搜寻脉冲周期和折叠轮廓。

2. Python 搜寻周期折叠相

脉冲周期 $f(t)$ 由 Taylor 多项式展开描述（不准确，离散的数据更准确的描述应该是差分多项式的牛顿级数展开）：

$f(t) = f(t_0)+(t-t_0)f'(t_0)+\frac{(t-t_0)^2f''(t_0)}{2}$

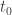那么以 $t_0$ 为时间零点，到达时间为 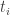$t_i$ 的光子相位，由上式两边乘以 $(t-t_0)$

$\phi_i = (t_i-t_0)[f(t_0)+ \frac{(t_i-t_0)f'(t_0)}{1} + \frac{(t_i-t_0)^2f''(t_0)}{2}]$

import numpy as np
import matplotlib.pyplot as plt
import pyfits as pf
import os
###########################
# read data from FITS file(optional)
# if this block is used, comment out next block then

#fpath = “/home/youli/Documents/crab_data/96802-01-21-00/faxbary_96802”
#hdulist = pf.open(fpath)

#tb = hdulist[1].data
#data = tb.field(2)

#hdulist.close()
###########################
# read data file from txt file
filename = ‘faxbary_0817_t1.txt’
data = np.loadtxt(filename)
##########################
# preset parameters
data = data – min(data)
N = len(data)
m = 100 # DOF for chi_square test
#nbin = 1000 # bin for histogram
b = N/m
f = np.arange(28.500,29.000,1e-2) # frequency searching range
chi_square = []

##########################

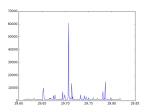
#search the best frequency utilizing the Chi-square test, where Chi-square is maxium

fbest = f[chi_square.index(max(chi_square))]

phi_tmp = np.mod(data*fbest,1.0)

p_num = np.histogram(phi_tmp,m)[0]

plt.figure(2)

p_num_x = np.arange(1.,m+1.,1)/m

#########################

# plot profile in 2 periods

#(if plot of 1 period is needed, comment out this block and use new commented block instead)

p_num_x_2_tmp = p_num_x + 1;p_num_x_2_tmp.tolist()

p_num_x_2 = p_num_x.tolist();p_num_2 = p_num.tolist()

p_num_x_2.extend(p_num_x_2_tmp);p_num_2.extend(p_num_2)

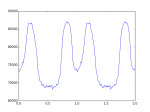
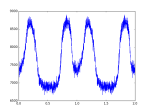
plt.plot(p_num_x_2,p_num_2)

#########################

#plot profile in one period

#plt.plot(p_num_x,p_num)

#########################

# print parameters

print “——————————–\n”,”INPUT PARAMETERS: \n”

print “input file: “,os.path.abspath(filename)

print “DOF of chi_square test: “,m

print “\nOUTPUT PARAMETERS: \n”

print “best frequency = “,fbest,”Hz”,”\nperiod = “,1/fbest,”s”

print “——————————–”

plt.show()

对自转频率的搜索利用的是 Chi-Square test。先计算光子的“相对相位”

$\Phi_i = \frac{(t_i-t_0)}{T} mod 1.0$

若信号不存在周期性，则光子的相位会呈现均匀分布

遇到的问题

log20160722

Posted on 2016-07-22 by Youli

iPhone 6 Lightning Connector Assembly was replaced:)

Such a low DPS, ugh~

LOG20160720

Posted on 2016-07-20 by Youli

This is the first day I officially move in the lab. My boss assigned few papers for me to read.

The strongest cosmic magnets: Soft Gamma-ray Repeaters and Anomalous X-ray Pulsars
Magnetars: properties, origin and evolution
Formation of very strongly magnetized neutron stars: Implications for Gamma-ray bursts

the first two papers are review papers of magnetars, which is probably the first subject I will work on. The last paper is the first paper suggesting the existing of magnetars.

I spent whole afternoon deleting and reinstalling computer system. Ubuntu 15.10 was installed. But I was told that this version of Ubuntu wouldn’t upgrade anymore. Reinstalling of Ubuntu 16.4 is on the to-do list.

A tiny tip of reinstalling system: be sure to copy some important info of previous system, like DNS service, IP Address. Rookie mistake was made by me XD

Mac下LateX文字环绕图片宏包wrapfig的安装及使用

Posted on 2015-10-21 by Youli

晚上写作业，无聊了没进展，怎么办，写日志。因为这是一件挺有意义也挺浪费时间的事儿。
你可能LaTeX代码敲得比我熟，哦；你可能用Tex Live Utility更新宏包，哦；你可能linux比我熟，哦；不打紧，这篇日志介绍一个不错的宏包，也记录一些操作细节，便于自己或别人重现，欢迎提建设性意见。

系统：OS X Yosemite 10.10.5
软件：XeTeX, Version 3.1415926-2.5-0.9999.3 (TeX Live 2013)
宏包下载：http://ctan.org/tex-archive/macros/latex/contrib/wrapfig/

使用的环境平易近人，和大多理工LaTeX使用者是一致的。
来，下面我们来手把手地做：

1# 下载宏包文件wrapfig.sty 并解压

2# 在Terminal中，复制宏包文件到制定目录
cd到你下载的目录/wrapfig/ 去（一般是/Download/啦）
cp -r wrapfig.sty /usr/local/texlive/2013/texmf-dist/tex/latex/base/

3# 刷新下LaTeX
sudo texhash
显示如下：
texhash: Updating /usr/local/texlive/2013/texmf-config/ls-R…
texhash: Updating /usr/local/texlive/2013/texmf-dist/ls-R…
texhash: Updating /usr/local/texlive/2013/texmf-var/ls-R…
texhash: Done.
就OK了

4#在你的论文中调用
\usepackage{wrapfig}

5#使用（含实例）
wrapfigure的用法：
\begin{wrapfigure}{行数}[位置][超出长度]{宽度}<图形>\end{wrapfigure}

实例：
\begin{wrapfigure}{l}{0.7\textwidth} \includegraphics[width=0.65\textwidth]{placeholder} \end{wrapfigure}

Blackhole

A unique dimension where I freely let loose my thoughts – as random and chaotic as they come

Category Archives: WorkLog